Bolschilstelling

Een massief, bolsymmetrisch lichaam kan worden samengesteld uit oneindig veel concentrische, infinitesimaal dunne bolschillen. Als een daarvan kan worden behandeld als een puntmassa, kunnen ze dat allemaal samen, dus de hele bol ook. Bekijk daartoe eerst een enkele bolschil en op die enkele bolschil een infinitesimaal smalle band.

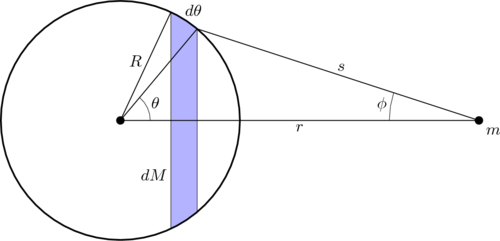
In het diagram verwijst ${\displaystyle \mathrm {d} \theta }$ naar de kleine hoek, niet naar de booglengte. De massa van de paarse band is ${\displaystyle dM}$ en de booglengte boven is ${\displaystyle R\mathrm {d} \theta }$. Uit de gravitatiewet van Newton en de cirkelsymmetrie van de band ten opzichte van ${\displaystyle m}$ volgt dat de radiale kracht uitgeoefend door de band in ${\displaystyle m}$ gelijk is aan:

${\displaystyle \mathrm {d} F_{r}={\frac {Gm\ \mathrm {d} M}{s^{2}}}\cos \phi }$

De totale kracht van de bolschil op ${\displaystyle m}$ wordt de som van de krachten die door alle banden samen worden uitgeoefend. Door de breedte van de banden te verkleinen en het aantal banden te vergroten wordt deze som tot een integraal:

${\displaystyle F_{r}=\int \mathrm {d} F_{r}=\int {\frac {Gm\cos \phi }{s^{2}}}\ \mathrm {d} M}$

Daarin zijn ${\displaystyle G}$ en ${\displaystyle m}$ constanten en mogen buiten de integraal worden gehaald:

${\displaystyle F_{r}=Gm\int {\frac {\cos \phi }{s^{2}}}\ \mathrm {d} M}$

De oppervlakte van de paarse band is

${\displaystyle 2\pi R\sin \theta \cdot R\ \mathrm {d} \theta =2\pi R^{2}\sin \theta \ \mathrm {d} \theta }$

Aangezien de totale oppervlakte van de bolschil gelijk is aan ${\displaystyle 4\pi R^{2}}$, is de massa ${\displaystyle dM}$ van de band:

${\displaystyle \mathrm {d} M={\frac {2\pi R^{2}\sin \theta }{4\pi R^{2}}}M\ \mathrm {d} \theta ={\tfrac {1}{2}}M\sin \theta \ \mathrm {d} \theta }$,

waarin ${\displaystyle M}$ de totale massa van de bolschil is. Dus volgt:

${\displaystyle F_{r}={\tfrac {1}{2}}GMm\int {\frac {\sin \theta \cos \phi }{s^{2}}}\ \mathrm {d} \theta }$

Met de cosinusregel:

${\displaystyle \cos \phi ={\frac {r^{2}+s^{2}-R^{2}}{2rs}}}$ en

${\displaystyle \cos \theta ={\frac {r^{2}+R^{2}-s^{2}}{2rR}}}$.

${\displaystyle \mathrm {d} \cos \theta \ =\ -\sin \theta \ \mathrm {d} \theta \ =\ \mathrm {d} \ {\frac {r^{2}+s^{2}-R^{2}}{2rs}}\ =\ -{\frac {s}{rR}}\ \mathrm {d} s}$

Substitueer dit in de integraal voor ${\displaystyle F_{r}}$:

${\displaystyle F_{r}={\frac {GMm}{2rR}}\int {\frac {\cos \phi }{s}}\ \mathrm {d} s={\frac {GMm}{4r^{2}R}}\int \left(1+{\frac {r^{2}-R^{2}}{s^{2}}}\right)\ \mathrm {d} s}$.

De integratievariabele ${\displaystyle s}$ loopt hierin van ${\displaystyle r-R}$ tot ${\displaystyle r+R}$.

${\displaystyle \int _{r-R}^{r+R}\left(1+{\frac {r^{2}-R^{2}}{s^{2}}}\right)\ \mathrm {d} s=\left[s-{\frac {r^{2}-R^{2}}{s}}\right]_{r-R}^{r+R}=4R}$,

zodat

${\displaystyle F_{r}=G{\frac {Mm}{r^{2}}}}$

Daaruit blijkt dat de zwaartekracht buiten de schil kan worden gedacht als veroorzaakt door een puntmassa ${\displaystyle M}$ in het middelpunt.

Om de zwaartekracht van een massieve bol met massa ${\displaystyle M}$ te berekenen wordt de zwaartekracht als gevolg van een bolschil met massa ${\displaystyle \mathrm {d} M}$ geïntegreerd:

${\displaystyle F_{\text{bol}}=\int {\frac {Gm}{r^{2}}}\ \mathrm {d} M}$

Een bolschil tussen de stralen ${\displaystyle x}$ en ${\displaystyle x+\mathrm {d} x}$ heeft een massa:

${\displaystyle \mathrm {d} M={\frac {4\pi x^{2}\ \mathrm {d} x}{{\frac {4}{3}}\pi R^{3}}}M=3{\frac {M}{R^{3}}}x^{2}\ \mathrm {d} x}$,

zodat

${\displaystyle F_{\text{bol}}=3{\frac {GMm}{r^{2}R^{3}}}\int _{0}^{R}x^{2}\ \mathrm {d} x=G{\frac {Mm}{r^{2}}}}$

Daaruit blijkt dat ook in dit geval de zwaartekracht buiten de bol gedacht kan worden als veroorzaakt door een puntmassa ${\displaystyle M}$ in het middelpunt.

Interessant is het geval met ${\displaystyle r<R}$, waarin de puntmassa binnen de bolschil ligt. Uit symmetrie-overwegingen volgt dat als de puntmassa in het middelpunt van de bolschil staat, de kracht nul moet zijn, maar dit geldt ook voor alle plaatsen binnen de schil.

De integraal loopt nu van ${\displaystyle R-r}$ tot ${\displaystyle R+r}$:

${\displaystyle F_{r}={\frac {GMm}{4r^{2}R}}\int _{R-r}^{R+r}{\frac {r^{2}+s^{2}-R^{2}}{s^{2}}}\mathrm {d} s=0}$

De schil oefent dus geen nettokracht uit op deeltjes aan de binnenkant. Informeel is dit ook als volgt te beredeneren. Verdeel een helft van de bolschil in kleine stukjes, en verdeel de andere helft door de stukjes via de massa ${\displaystyle m}$ daarop te projecteren. Een stukje schil dicht bij de massa ${\displaystyle m}$ wordt geprojecteerd op een groter stuk onder dezelfde ruimtehoek, aan de andere kant van ${\displaystyle m}$, en op een grotere afstand. De massaverhouding van de twee stukjes is het kwadraat van de verhouding van de afstanden van ${\displaystyle m}$, want de correctiefactoren voor de hoek waaronder de twee richtingslijnen de bolschil snijden komen overeen. De effecten van een grotere massa en een grotere afstand worden door de omgekeerde kwadratenwet tegen elkaar weggestreept. Beide stukjes oefenen op ${\displaystyle m}$ dus krachten van gelijke grootte in tegengestelde richtingen uit, dus per saldo geen kracht, en voor alle paren stukjes samen dus ook niet.

Het effect van een bolsymmetrische bolschil met positieve dikte, binnenste straal ${\displaystyle R_{a}}$ en buitenste straal ${\displaystyle R_{b}}$, kan ook worden berekend. De zwaartekracht binnen en buiten de bolschil wordt op dezelfde manier gevonden als bij een dunne schil. De zwaartekracht in de schil zelf, dus voor ${\displaystyle R_{a}<r<R_{b}}$, staat hieronder uitgerekend.

Uit het bovenstaande blijkt dat alleen de dikke bolschil tussen ${\displaystyle R_{a}}$ en ${\displaystyle r}$ bijdraagt aan de zwaartekracht. Net als boven kan deze dikke bolschil in gedachten worden samengesteld uit vele concentrische dunne bolschillen met straal ${\displaystyle R_{a}<R<r}$. De bijdrage aan de zwaartekracht van een zo'n schil is:

${\displaystyle \mathrm {d} F_{r}={\frac {Gm}{r^{2}}}\mathrm {d} M_{R}}$

Daarin is

${\displaystyle \mathrm {d} M_{R}=4\pi R^{2}\rho \ \mathrm {d} R}$,

met ${\displaystyle \rho ={\frac {M}{{\frac {4}{3}}\pi (R_{b}^{3}-R_{a}^{3})}}}$ de massadichtheid. Dus is

${\displaystyle F_{r}={\frac {4\pi Gm}{r^{2}}}\int _{R_{a}}^{r}R^{2}\rho \ \mathrm {d} R=G{\frac {Mm}{r^{2}}}\int _{R_{a}}^{r}{\frac {3R^{2}}{R_{b}^{3}-R_{a}^{3}}}\ \mathrm {d} R=G{\frac {Mm}{r^{2}}}{\frac {r^{3}-R_{a}^{3}}{R_{b}^{3}-R_{a}^{3}}}}$

Een massieve bol met straal ${\displaystyle R}$ kan gezien worden als een speciaal geval van een dikke bolschil met ${\displaystyle R_{a}=0}$ en ${\displaystyle R_{b}=R}$:

Dus geldt voor ${\displaystyle r<R}$:

${\displaystyle F_{r}=G{\frac {Mm}{R^{2}}}{\frac {r}{R}}={\frac {GMmr}{R^{3}}}}$